매니퓰레이터

궤적 생성 방법

드디어 제어를 로봇에 직접 적용할 수 있는 파트입니다. 물론, 직전에 배운 기구학, 동역학, 동역학 파라미터 추정 등이 로봇 매니퓰레이터 제어 시에 필요 없는 것이 절대 아닙니다. 다만, 본 장을 포함해 앞으로 나올 위치기반 제어, 토크 기반 제어, 힘 제어, 그리고 컴플라이언스 제어까지 모든 제어 방법을 하나의 요리라고 한다면, 지금까지 공부한 것들은 로봇의 상태를 이해하기 위한 재료를 준비한 것이기 때문이죠. 동역학 기반 위치제어나 힘제어를 수행하기 위해서는 로봇 매니퓰레이터 작업상의 시작위치와 종료위치 사이의 궤적(trajectory)을 시간에 대한 함수로 정의하여 제어를 수행하는 것이 좋습니다. 당연하게도, 이는 매 제어 샘플링마다 연속적인 제어 입력 값이 인가될 수 있어야 상대적으로 좋은 제어 ..

동역학 파라미터들에 관한 선형 동역학

지금까지 알아본 동역학/역동역학 산출 방식은 모두 파라미터들을 기반으로 계산됨을 알 수 있습니다. 하지만, 실제로는 모든 파라미터들을 정확하게 얻어내기 쉽지 않습니다. 로봇 동역학 모델 식(2.48)을 다시 보면서 얘기하자면, $M(q)\ddot{q}+C(q, \dot{q})\dot{q}+g(q)+d=\tau$ 본 식을 정확하게 구현함에 있어서 가장 어려운 부분은 로봇 링크들의 질량 $m$, 링크 별 무게중심까지의 거리 $r$, 링크 관성 $I$, 관절 구동기 관성 $I_m$, 관절의 마찰계수 $F_s, F_v$와 같은 동역학 파라미터를 정확하게 알기 어려운 것입니다. 그래서 동역학 모델 식 구조를 활용하여 동역학 파라미터들을 추정하는 문제는 오래도록 연구되고 있으며, 이에 대한 예제를 가지고 고찰해보고..

Dynamics and Inverse dynamics

Dynamics and Inverse dynamics 로봇 동역학은 매니퓰레이터에 작용하는 힘/토크들과 관절 가속도 간의 관계를 기술 한 것입니다. 용도에 따라서 다음과 같이 2가지로 구분됩니다. 순동역학 (forward dynamics or direct dynamics) : 주어진 입력 힘/토크에 대해서 로봇 운동 관절의 가속도를 산출하는 것. 부가적으로 수치적분 알고리즘을 적용하여 로봇 운동관절의 속도/위치 정도까지도 확정하여 얻는 과정을 포함하여 forward dynamics라고 한다. 역동역학 (inverse dynamics) : 주어진 운동 관절의 가속도 정보로 부터 로봇의 힘/토크를 산출하는 것. 이를 확장하여 로봇 운동관절의 위치/속도/가속도가 주어져 있을 때, 상응하는 로봇 힘/토크를 대수..

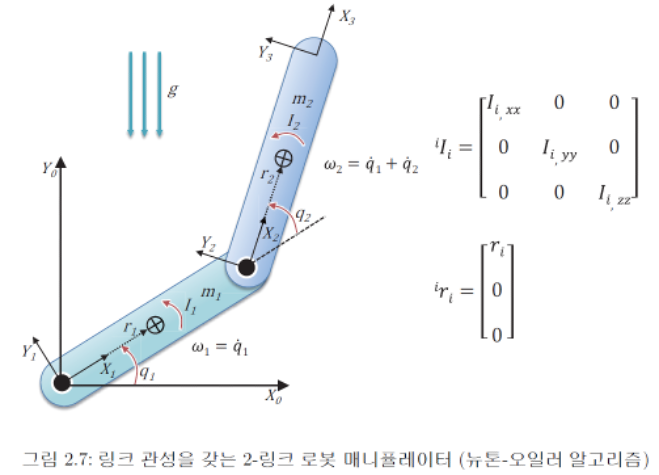
동역학 - 뉴턴 오일러 운동방정식 3

동역학 - 뉴턴 오일러 운동방정식 3 지금까지 알아본, 각 링크의 관절에 설정된 좌표계들 사이의 좌표변환 관계를 고려한 뉴턴-오일러 동역학 알고리즘은 다음과 같습니다. 1. 매니퓰레이터의 글로벌(0번째) 기준 좌표계에 대한 초기 조건을 설정한다. * 초기 직진가속도를 위와 같이 설정함에 따라 중력가속도는 모든 링크들에 자연스럽게 적용됩니다. 2. $i=1$부터 $i=n$까지 전진 순차를 적용합니다. 3. 매니퓰레이터의 끝단의 힘/모멘트에 관한 말단 조건을 가지고 $i=n$부터 $i=1$까지 후진 역차를 적용합니다. 4. $i$번째 관절에서의 힘/토크는 구동기 특성을 고려하여 다음과 같이 결정됩니다. 이제 2링크 매니퓰레이터의 동역학 모델에 적용해보겠습니다. 다음 그림과 같은 매니퓰레이터 시스템에 적용하기..