동역학 - 뉴턴 오일러 운동방정식 3
지금까지 알아본, 각 링크의 관절에 설정된 좌표계들 사이의 좌표변환 관계를 고려한 뉴턴-오일러 동역학 알고리즘은 다음과 같습니다.
1. 매니퓰레이터의 글로벌(0번째) 기준 좌표계에 대한 초기 조건을 설정한다.
* 초기 직진가속도를 위와 같이 설정함에 따라 중력가속도는 모든 링크들에 자연스럽게 적용됩니다.
2. $i=1$부터 $i=n$까지 전진 순차를 적용합니다.
3. 매니퓰레이터의 끝단의 힘/모멘트에 관한 말단 조건을 가지고 $i=n$부터 $i=1$까지 후진 역차를 적용합니다.
4. $i$번째 관절에서의 힘/토크는 구동기 특성을 고려하여 다음과 같이 결정됩니다.
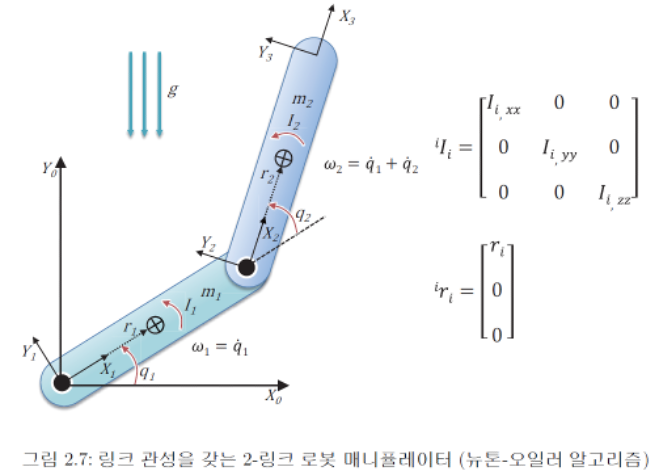
이제 2링크 매니퓰레이터의 동역학 모델에 적용해보겠습니다.
다음 그림과 같은 매니퓰레이터 시스템에 적용하기 위해, 최대한 단순화 시키기 위해 다음과 같이 관성 모멘트는 대각 성분만 가진다고 가정합니다.
그리도 무게중심 벡터는 각좌표계의 X축을 따라서 $r_i$만큼 떨어져 있다고 가정합니다.
위에서 설명한 것과 같이,
첫번째 - 글로벌 기준좌표계에 대한 초기 조건을 설정합니다 (이때, $g=9.8 m/s^2$).
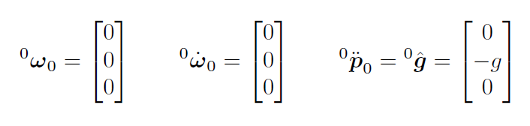 |
두번째 - $i=1$에 대한 전진 순차를 적용합니다 (식 2.40 ~ 2.42).
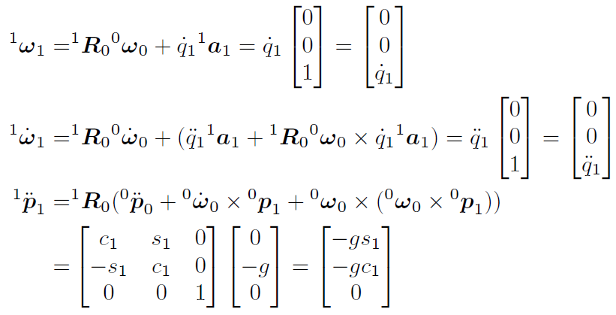 |
 |
 |
세번째 - $i=2$에 대한 후진 역차를 적용합니다 (식 2.43 ~ 2.44).
 |
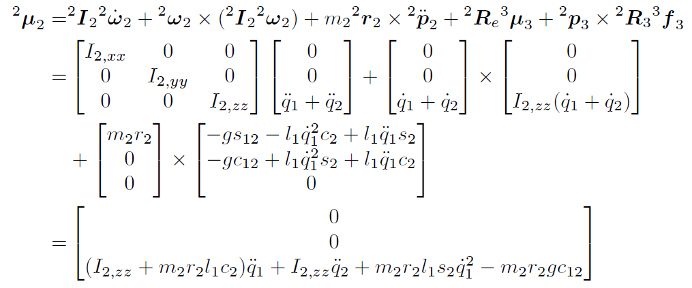 |
 |
 |
네번째 - 관절 1, 2에 대한 힘/토크 방정식을 구합니다 (식 2.45).
 |
 |
이와 같이 질량을 가진 2링크 시스템에 적용까지 해보았습니다.
결국 뉴턴-오일러 알고리즘은 반복적인 연산을 통해 직진/회전 속도, 가속도를 구하고 이를 기반으로 힘과 직진운동 간의 관계, 그리고 모멘트와 회전운동 간의 관계를 알 수 있습니다.
이러한 뉴턴-오일러 알고리즘의 장점 중 하나는 자연스럽게 관절 구동기의 관성력과 다양한 마찰력을 포함할 수 있다는 것입니다.
또한 이를 통해 얻어진 로봇 동역학 모델 또한 잘 알려진 로봇 동역학 (식 (2.5))으로 정리 가능합니다.
이상입니다.
* 본 글은 "실험로보틱스 교재 I(매니퓰래이션 및 비젼), 한국로봇학회, 제어로봇시스템학회, 한국로봇산업진흥원 "의 내용을 공부하면서 정리한 내용을 포스팅 한 것 입니다.
'Robot Theory > Manipulator Theory' 카테고리의 다른 글
| 동역학 파라미터들에 관한 선형 동역학 (0) | 2022.08.14 |
|---|---|
| Dynamics and Inverse dynamics (0) | 2022.07.25 |
| 동역학 - 뉴턴 오일러 운동방정식 2 (0) | 2022.07.04 |
| 동역학 - 뉴턴 오일러 운동방정식 1 (0) | 2022.06.16 |
| C(q, /dot{q})과 크리스토펠 심볼 식 활용 (0) | 2022.06.16 |