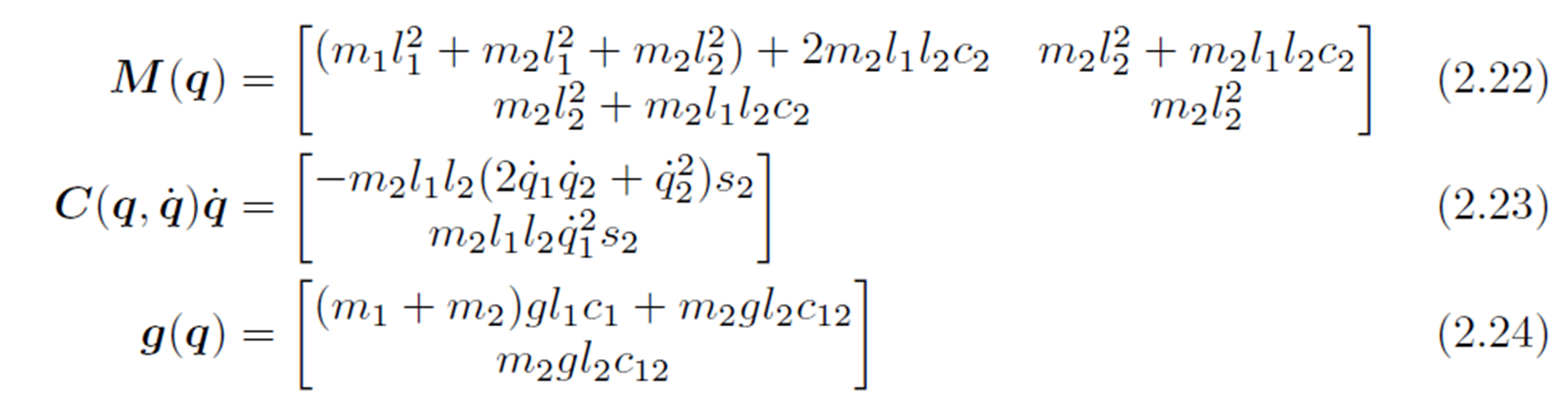동역학 - Appendix
코리올리 및 구심력 벡터로부터 행렬 $C(q, \dot{q})$와 속도벡터 $\dot{q}$을 분리하는 방법이 무수히 많은데, 여기서는 크리스토펠 심볼 식을 이용하여 $C(q, \dot{q})$의 유일한 형태를 찾는 방법에 대해서 설명하고 있습니다(이전 포스팅).
식 (2.22)의 행렬요소별 $q$에 대한 의존성을 확인해 보면 $M_{11}(q_2), M_{12}(q_2), M_{21}(q_2)$를 확인할 수 있으며, $M_{22}$는 관절 변수에 대한 의존성 없이 상수임을 알 수 있습니다.
* $c_2 = cos(q_2)$ 이므로, $M_{22}$만 상수 취급 가능함
이를 활용하면 다음과 같이 $C(q, \dot{q})$에 대한 유일해를 찾을 수 있습니다.
이상입니다.
* 본 글은 "실험로보틱스 교재 I(매니퓰래이션 및 비젼), 한국로봇학회, 제어로봇시스템학회, 한국로봇산업진흥원 "의 내용을 공부하면서 정리한 내용을 포스팅 한 것 입니다.
'Robot Theory > Manipulator Theory' 카테고리의 다른 글
| 동역학 - 뉴턴 오일러 운동방정식 2 (0) | 2022.07.04 |
|---|---|
| 동역학 - 뉴턴 오일러 운동방정식 1 (0) | 2022.06.16 |
| 동역학 - 라그랑주 운동방정식 2 (0) | 2022.06.02 |
| 동역학 - 라그랑주 운동방정식 1 (0) | 2022.05.16 |
| 동역학 - Introduction (0) | 2022.05.13 |