동역학

동역학 파라미터들에 관한 선형 동역학

지금까지 알아본 동역학/역동역학 산출 방식은 모두 파라미터들을 기반으로 계산됨을 알 수 있습니다. 하지만, 실제로는 모든 파라미터들을 정확하게 얻어내기 쉽지 않습니다. 로봇 동역학 모델 식(2.48)을 다시 보면서 얘기하자면, $M(q)\ddot{q}+C(q, \dot{q})\dot{q}+g(q)+d=\tau$ 본 식을 정확하게 구현함에 있어서 가장 어려운 부분은 로봇 링크들의 질량 $m$, 링크 별 무게중심까지의 거리 $r$, 링크 관성 $I$, 관절 구동기 관성 $I_m$, 관절의 마찰계수 $F_s, F_v$와 같은 동역학 파라미터를 정확하게 알기 어려운 것입니다. 그래서 동역학 모델 식 구조를 활용하여 동역학 파라미터들을 추정하는 문제는 오래도록 연구되고 있으며, 이에 대한 예제를 가지고 고찰해보고..

Dynamics and Inverse dynamics

Dynamics and Inverse dynamics 로봇 동역학은 매니퓰레이터에 작용하는 힘/토크들과 관절 가속도 간의 관계를 기술 한 것입니다. 용도에 따라서 다음과 같이 2가지로 구분됩니다. 순동역학 (forward dynamics or direct dynamics) : 주어진 입력 힘/토크에 대해서 로봇 운동 관절의 가속도를 산출하는 것. 부가적으로 수치적분 알고리즘을 적용하여 로봇 운동관절의 속도/위치 정도까지도 확정하여 얻는 과정을 포함하여 forward dynamics라고 한다. 역동역학 (inverse dynamics) : 주어진 운동 관절의 가속도 정보로 부터 로봇의 힘/토크를 산출하는 것. 이를 확장하여 로봇 운동관절의 위치/속도/가속도가 주어져 있을 때, 상응하는 로봇 힘/토크를 대수..

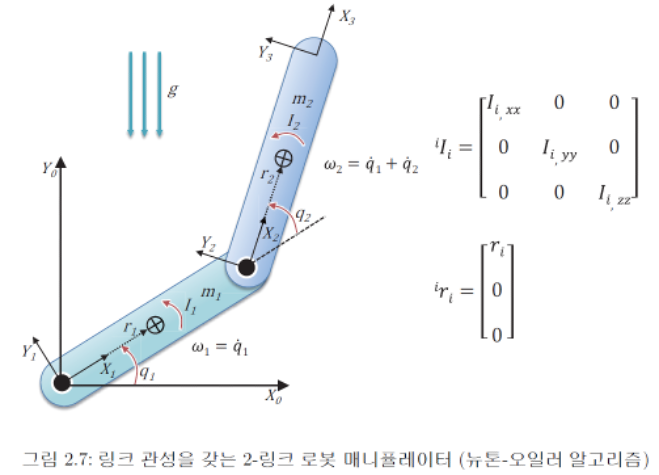
동역학 - 뉴턴 오일러 운동방정식 3

동역학 - 뉴턴 오일러 운동방정식 3 지금까지 알아본, 각 링크의 관절에 설정된 좌표계들 사이의 좌표변환 관계를 고려한 뉴턴-오일러 동역학 알고리즘은 다음과 같습니다. 1. 매니퓰레이터의 글로벌(0번째) 기준 좌표계에 대한 초기 조건을 설정한다. * 초기 직진가속도를 위와 같이 설정함에 따라 중력가속도는 모든 링크들에 자연스럽게 적용됩니다. 2. $i=1$부터 $i=n$까지 전진 순차를 적용합니다. 3. 매니퓰레이터의 끝단의 힘/모멘트에 관한 말단 조건을 가지고 $i=n$부터 $i=1$까지 후진 역차를 적용합니다. 4. $i$번째 관절에서의 힘/토크는 구동기 특성을 고려하여 다음과 같이 결정됩니다. 이제 2링크 매니퓰레이터의 동역학 모델에 적용해보겠습니다. 다음 그림과 같은 매니퓰레이터 시스템에 적용하기..

동역학 - 뉴턴 오일러 운동방정식 1

동역학 - 뉴턴 오일러 운동방정식 들어가기 라그랑주 운동방정식은 해석적으로 사용할 수 있다는 장점이 있지만, 미분 연산을 요구하므로 3자유도 이상의 다관절 로봇 매니퓰레이터의 경우에는 적용하기 까다롭다는 단점이 있습니다. 그러나 뉴턴-오일러 운동방정식은 미분연산을 요구하지 않으면서 대수학만으로 로봇 동역학 모델을 얻을 수 있습니다. 물론 뉴턴-오일러 운동방정식으로도 해석적인 형태의 로봇 동역학 모델을 얻을 수 있지만, 이를 위한 목적보다는 6자유도 등과 같은 다자유도 로봇의 동역학 모델을 수치적으로 얻을 때 주로 이용됩니다. 이러한 방법은 '전진 순차', '후진 역차' 방법으로 힘/모멘트를 계산하는 방식으로 구성됩니다. 이상입니다. * 본 글은 "실험로보틱스 교재 I(매니퓰래이션 및 비젼), 한국로봇학회..