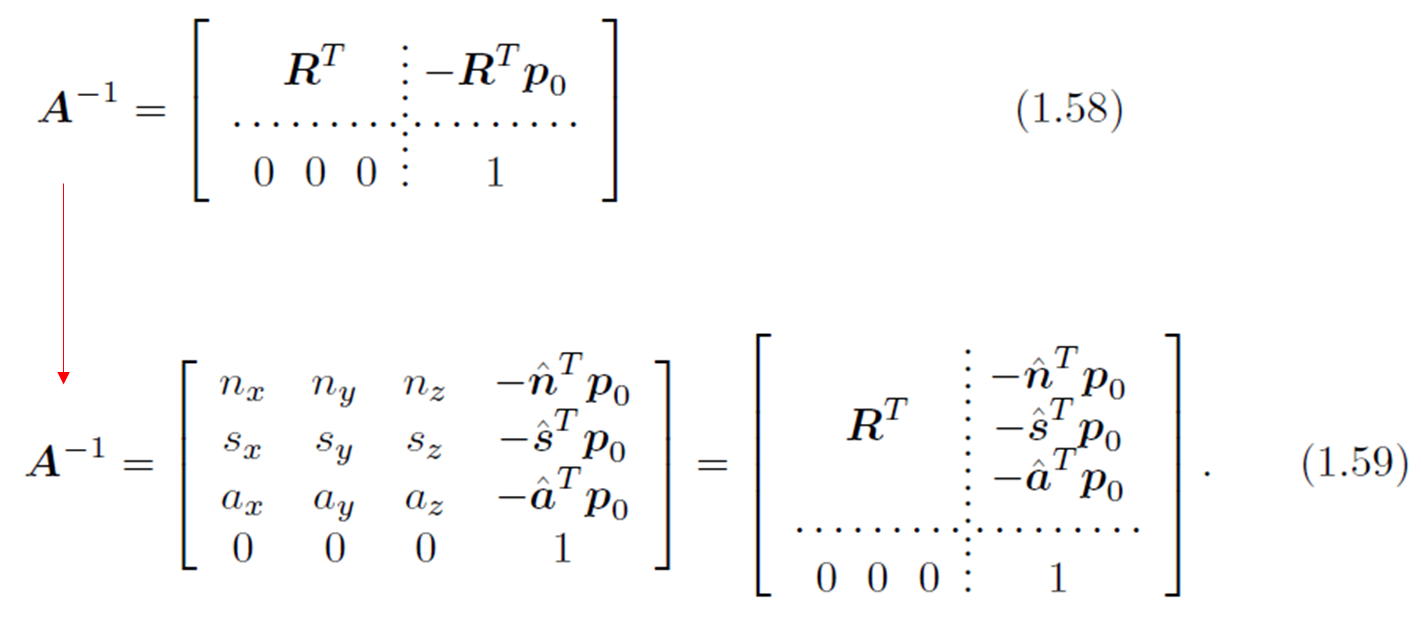동차 변환 (Homogeneous Transform)
동차 변환은 좌표 변환(좌표 이동 및 크기 조정)를 나타내는, 간결한 형태를 의미합니다.
다음 그림 1.7과 같이 점 p를 강체 상의 임의의 한 점이라고 할 때,

고정좌표계 O-xyz 기준일 때:강체 좌표계 O′-x′y′z′ 기준일 때:
두 좌표계 간의 관계는 고정 좌표계와 강체 좌표계의 좌표 변환으로 정의할 수 있으며, 다음 식 (1.42)와 같이 표현 가능합니다.
(3x1)vector = (3x1)vector + (3x3)Mat * (3x1)vector
이와 같은 식 (142)의 역변환은 다음과 같이 정의가 가능합니다.
이와 같이 동차 변환은 이동, 회전 둘을 동시에 수행하는 간결성의 장점을 갖기 때문에 로봇 공학 뿐만 아니라 강체의 상태를 수학적으로 표현하는 다양한 곳에서 많이 활용합니다.
동차 변환 행렬에서는 식 (1.40)의 위치 벡터에서 네번째 요소 $\omega$ 즉, 크기 조정 상수가 추가됩니다.
식 (1.46)를 살펴보면, 결국 물리적 좌표는 $\omega$로 인해 동차 좌표로 표현이 가능하다는 것입니다.
다행인 점은, 로봇 기구학에서는 $\omega$가 변하지 않고 1의 단위량을 가지게 되므로 굳이 신경쓰지 않아도 됩니다.
그렇지만, 다른 분야에서는 임의의 양수 값을 갖는 경우가 많다고 하니, 알아두면 좋을 것 같습니다.
이와 같이 동차 변환을 활용해서 회전만을 위한 행렬 (1.49 - 1.51), 이동 만을 위한 행렬 (1.52)을 만들 수 있다.
결과적으로 식(1.42)를 동차 좌표계와 동차 행렬을 조합하여 가장 많이 쓰는, 최종 형태가 만들어진다.
이에 대한 역변환 행렬은 다음과 같이 표현이 가능하며, $(A^{-1})$은 다음과 같이 정의된다.
이상입니다.
* 본 글은 "실험로보틱스 교재 I(매니퓰래이션 및 비젼), 한국로봇학회, 제어로봇시스템학회, 한국로봇산업진흥원 "의 내용을 공부하면서 정리한 내용을 포스팅 한 것 입니다.
'Robot Theory > Manipulator Theory' 카테고리의 다른 글
| 동역학 - 라그랑주 운동방정식 1 (0) | 2022.05.16 |
|---|---|
| 동역학 - Introduction (0) | 2022.05.13 |
| 기구학 - 여유자유도(Redundancy) (0) | 2022.05.09 |
| 기구학 - Velocity Kinematics (0) | 2022.04.27 |
| 기구학 - Kinematics (0) | 2022.04.25 |